I’m back! It’s been a while since I’ve been on this site because I’ve found myself under some financial trouble and I’ve been stressed BUT I wanted to take this opportunity to talk about something I love dearly: dihedral groups!
Consider the symmetries of a square:
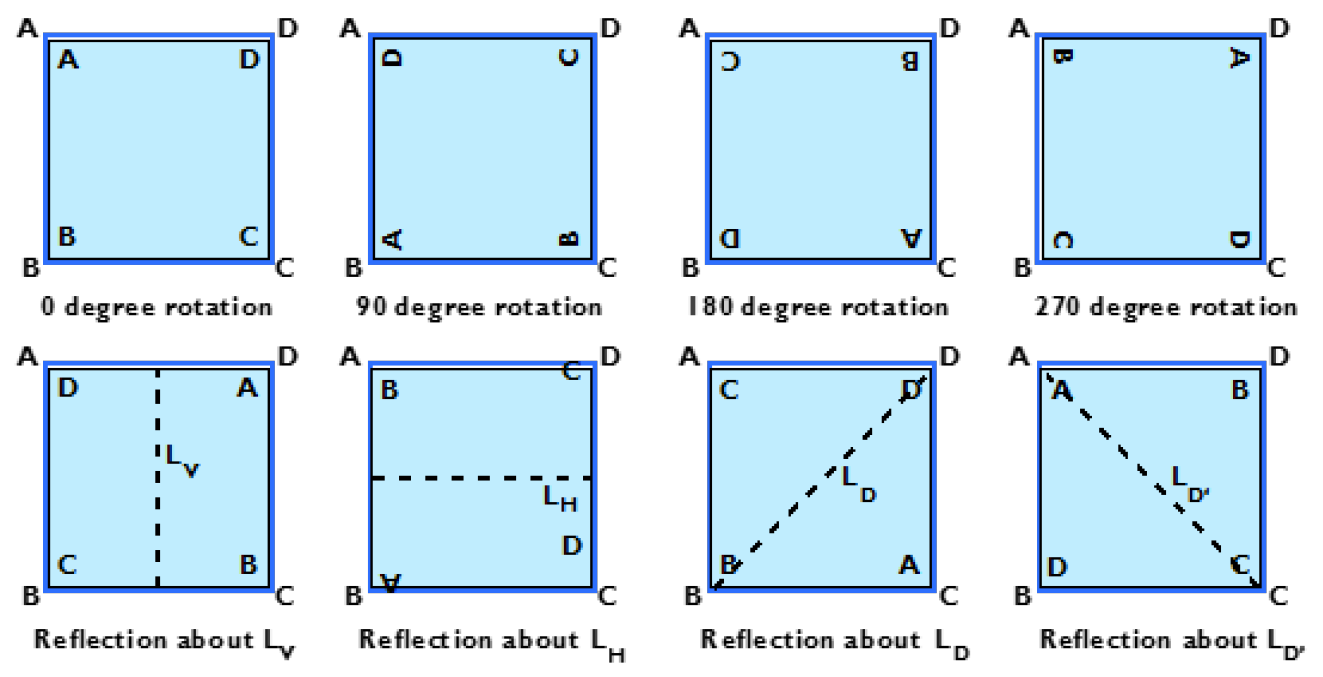
We can see that there are 4 reflections and 3 rotations, as well as the act of doing nothing at all. Together, we have 8 total symmetries, and in fact, these are all of the possible symmetries. What this means is that if we do one of these symmetric moves and then do another one, we will have not changed the square, and therefore doing these two moves is the same as doing just one of the 8 symmetries on its own. For example, doing a 90 degree rotation followed by a 180 degree rotation is the same as doing a 270 degree rotation. Also, doing a 90 degree rotation followed by a reflection across the vertical axis is the same as doing a reflection across a diagonal axis.
So in other words, we can define a function that takes two symmetries of a square as input and which outputs another symmetry. Since standard multiplication is a function taking two numbers and outputting another number, it makes sense to borrow the notation of multiplication for this function. Our symmetry function satisfies a few useful properties:
- Closure: As explained above, for any two symmetries, the function will spit out another symmetry
- Identity: There is a symmetry (namely, the “do nothing” symmetry) such that when it is input into the function with another symmetry, the function will always simply output the other symmetry
- Associativity: For any symmetries a, b, and c, (ab)c = a(bc)
- Inverses: For every symmetry, there is a symmetry that undoes it. For example, rotating a square by 270 degrees undoes rotating it by 90 degrees, and doing a reflection a second time after doing it once undoes the first reflection
These 4 properties are so important that any set of objects with a function defined on it that satisfies all of these properties has a special name: they’re called groups and they’re really freaking awesome. The symmetries of a square as a group is called D~8~, since there are 8 total symmetries. Sometimes you might see it called D~4~, since squares have 4 sides, but I think this convention is a bit silly. In the same way, D~6~ is the symmetries of an equilateral triangle, D~10~ is the symmetries of a regular pentagon, and so forth. In general, D~2n~ is the symmetries of a regular n-gon.
Now, one interesting thing is that groups can contain each other. For example, consider an octagon. Since there are squares hidden within the points of octagons, if we pick a square we can see that all of the symmetries of that square are present in the symmetries of of the octagon, so it is possible to throw out all of the other symmetries. What we would be left with is just the symmetries of a square. What this means is that D~8~ is contained in D~16~. You can play similar games to show that there are lots of groups contained inside the dihedral groups.
The last thing I want to talk about regarding these things are their subgroup lattices. Oftentimes mathematicians want to picture the internal structure of a group. One of the ways they might do this is by writing down all of the subgroups of a group they’re studying onto a piece of paper, and then connecting any two with a line if one of them is a subgroup of the other that doesn’t have a subgroup between them. The resulting picture is called a subgroup lattice, and I’ve left some dihedral group lattices below because I think they’re pretty.
two cute dihedral subgroup lattices holding hands and cuddling
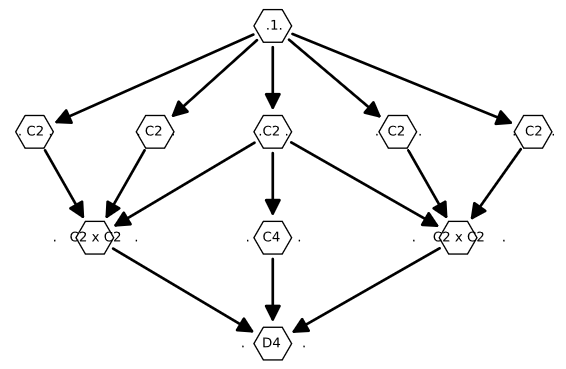
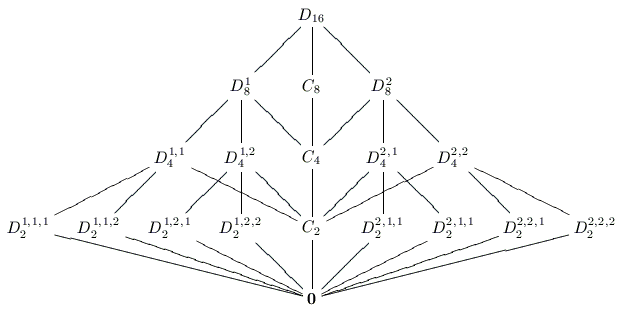
Anyway this has been gushposting with your host, yewler. Maybe next mega I might talk about more specific details that make these things cool.
Now you may commence in the posting
Join our public Matrix server!
https://matrix.to//#/#tracha-space:transfem.dev
https://rentry.co/tracha#tracha-rooms
As a reminder, please do not discuss current struggle sessions in the mega. We want this to be a little oasis for all of us and the best way to do that is not to feed into existing conflict on the site.
Also, be sure to properly give content warnings and put sensitive subjects behind proper spoiler tags. It's for the mental health of not just your comrades, but yourself as well.
Here is a screenshot of where to find the spoiler button.



Feeling extra gay this month idk why